Sorting algorithms 📚

Nearly every standard library offers data structures that can be sorted without really thinking about it. Still, it might come in handy to know about commonly used sorting algorithms or even implement some of them yourself as an exercise. After all, most sorting algorithms make heavy use of array indexing and recursion, and for this reason alone, they are often used as a medium to learn about and apply these concepts.

Even though sorting algorithms can be categorized by just a handful of different methods, there are hundreds of variations out there. Some algorithms are more efficient than others. You can compare their efficiency by both time complexity and memory consumption. It is worth noting that some sorting algorithms may perform worse in certain situations while, on average, they perform better than others. Finally, a stable sorting algorithm is expected to preserve the order of elements considered to be equal.

As you can tell, choosing the right sorting algorithm may not always be so easy. For this reason, I have compiled the following list, including implementation details for future reference:

Name	Best Average Worst	Memory	Stable	Method
Quicksort	$n \log n$ $n \log n$ $n^2$	$\log n$	No	Partitioning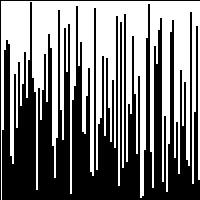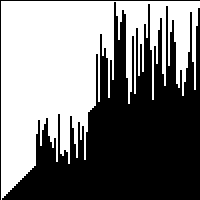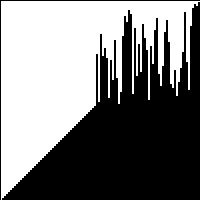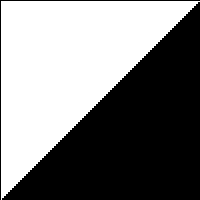
Merge sort	$n \log n$ $n \log n$ $n \log n$	$n$	Yes	Merging
Heapsort	$n \log n$ $n \log n$ $n \log n$	1	No	Selection
Insertion sort	$n$ $n^2$ $n^2$	1	Yes	Insertion
Selection sort	$n^2$ $n^2$ $n^2$	1	No	Selection
Shellsort	$n \log n$ $n^{4 \over 3}$ $n^{3 \over 2}$	1	No	Insertion
Bubble sort	$n$ $n^2$ $n^2$	1	Yes	Exchanging

Further reading​

Further reading